Stéphane Pelle Responsable de la Cellule Pédagogique et de Recherche en Informatique 01.64.15.3159

5 juillet 2001

Table des matières

1) La méthode HBDS *

1) La méthode HBDS

La méthode HBDS (Hypergraph Based Data Structure) est une méthode de modélisation des données relative à la théorie des hypergraphes. Elle a fait l'objet de la thèse du Professeur Bouillé en 1977.

1.1) Les éléments fondamentaux

Cette méthode présente les trois éléments fondamentaux suivants : classe, attribut et lien.

Une classe est un ensemble d'éléments appelés objets. Elle est représentée par une ellipse dont un des foyers symbolise un objet quelconque de la classe. Les objets de cette classe sont caractérisés par des attributs, représentés par des carrés reliés par un trait au foyer. Les objets d'une classe peuvent être en relation avec des objets de la même classe ou d'autres classes grâce à la notion de "lien entre classes". Un lien entre classes est potentiel (il peut ne pas être réalisé pour certains objets) et est représenté par une flèche entre les foyers des deux classes concernées. Le lien inverse est implicite.

1.2) Les objets

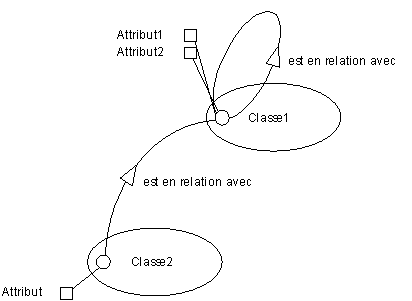
Sauf besoin de précision particulière, les objets, les valeurs des attributs d'objets et leurs liens ne sont pas représentés sur le modèle. On peut par contre préciser, entre parenthèses, la liste des valeurs prises par chaque attribut énuméré. Une fois n'est pas coutume, voici un exemple de modèle avec quelques objets pour bien clarifier le discours.

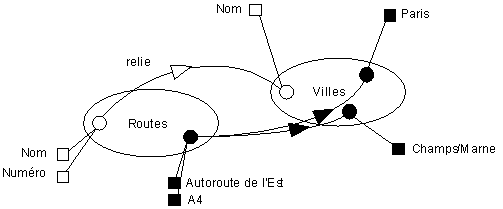
La lecture de ce modèle se fait comme suit :

- une route a un nom et un numéro ;

- une ville a un nom ;

- une route relie des villes.
 
 

1.3) Les attributs composés

Pour simplifier le schéma, on peut regrouper les attributs d'une classe pour faire un attribut composé. Réciproquement, chaque attribut peut être considéré comme un attribut composé et donc être décomposé au fur et à mesure des connaissances acquises. On commence donc toujours par des attributs simples.

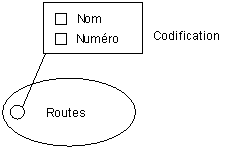
La lecture de ce modèle se fait comme suit :

- une route a une codification à savoir un nom et un numéro

1.4) Les hyperclasses

Comme précédemment, on peut regrouper des classes pour faire une hyperclasse portant les attributs et les liens communs à un ensemble de classes. Réciproquement, chaque classe peut être considérée comme une hyperclasse et décomposée au fur et à mesure des connaissances acquises. On commence donc toujours par représenter uniquement des classes.

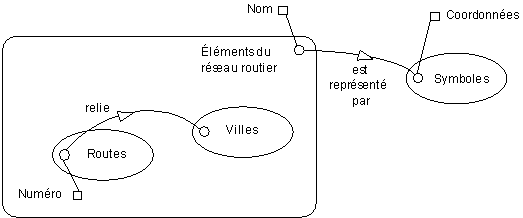
La lecture de ce modèle se fait comme suit :

- un symbole a des coordonnées ;

- les routes et les villes sont des éléments du réseau routier ;

- un élément du réseau routier a un nom et est représenté par des symboles

- une route a un numéro ;

- une route relie des villes.

2) La notion de MCD Géographique

2.1) La notion de MCD

En résumé, un MCD (Modèle Conceptuel de Données) est un schéma HBDS qui décrit les types d'éléments HBDS que l'on peut utiliser pour modéliser les données :
 

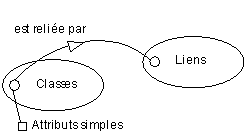Ce MCD autorise les attributs sur les classes et les liens entre classes mais interdit l'usage des hyperclasses et les attributs composés.

Un modèle HBDS qui respecte les règles édictées par un MCD s'appelle un Schéma Conceptuel de Données. Voici un exemple de SCD conforme au MCD précédent :

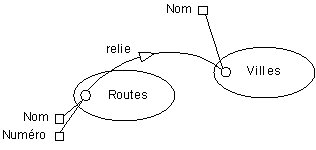
2.2) La notion de MCD Géographique

Un MCD Géographique est un MCD en 2 parties : une partie regroupant les classes sémantiques et une partie regroupant les classes géométriques. Tous les Systèmes d'Information Géographique possède un MCD (explicite ou non). Un MCD général pour tous les SIG est présenté ci-dessous. On remarquera principalement que les classes d'objets géométriques sont communes à tous les SCD conformes à ce MCD et que les objets complexes ne sont pas représentés directement par la géométrie.
 
 

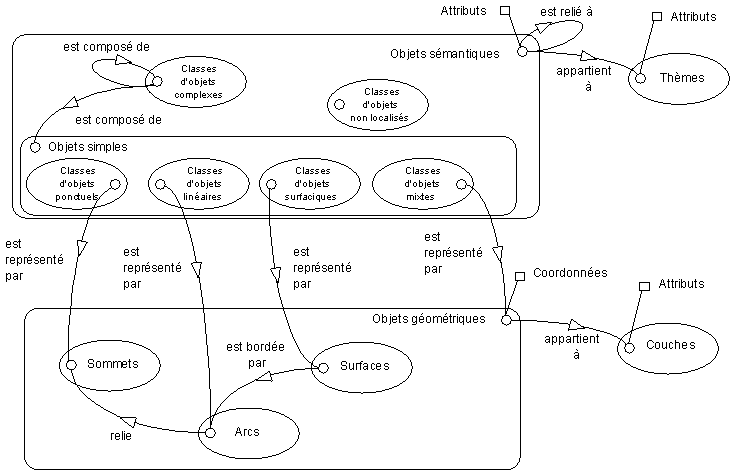
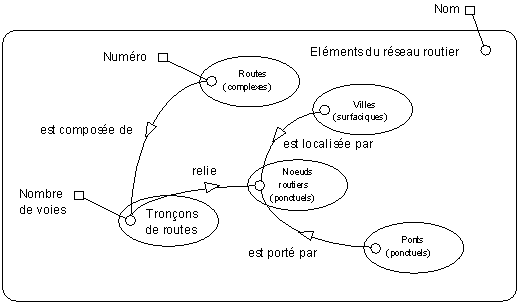
Le SCD Géographique suivant est conforme au MCD Géographique précédent. On notera toutefois que tous les types d'éléments ne sont pas utilisés et que les classes sémantiques faisant partie du même thème ont été regroupées au sein d'une hyperclasse qui porte en substance le nom du thème.

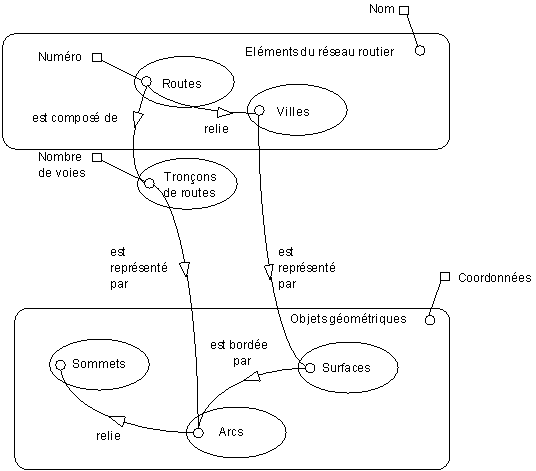
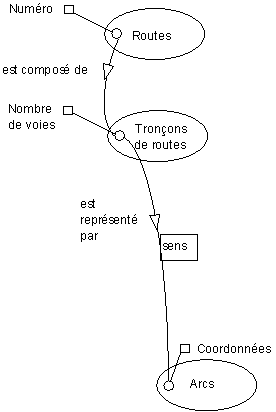
La lecture de ce SCD se fait comme suit :

- un élément du réseau routier a un nom ;

- les routes et les villes sont des éléments du réseau routier ;

- une route est composée de tronçons de routes (c'est un objet complexe) ;

- une route relie une ville (lien sémantique) ;

- un tronçon de route a un nombre de voies ;

- un tronçon de route est représenté par des arcs (c'est un objet simple linéaire) ;

- une ville est représentée par des surfaces (c'est un objet simple surfacique).

3) La gestion de plusieurs échelles et les symboles

3.1) La présence des classes géométriques

Un MCD Géographique contient nécessairement une partie géométrique figée : une seule classe d'arcs, etc... De ce fait, tous les SCD correspondants contiendront peu ou prou les mêmes classes géométriques. On peut donc omettre ces classes en indiquant simplement sur chaque classe la nature des objets qu'elle contient : ponctuels, linéaires, surfaciques, mixtes, complexes ou non localisés.

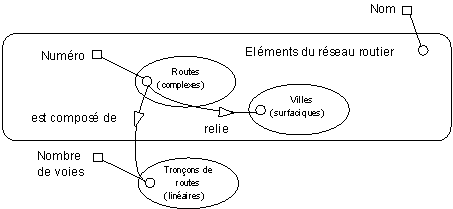
3.2) Une base de données multi-échelle ?

Dans le cas d'une base de données multi-échelle, la géométrie de chaque objet va dépendre de l'échelle de saisie ou de représentation : une ville de 10 000 habitants sera tantôt représentée par une surface, tantôt représentée par un symbole attaché à un point. Comme précédemment, il est inutile de faire apparaître les classes géométriques mais il faut au contraire préciser la représentation des objets dans un glossaire décrivant le contenu de chaque classe !

3.3) Les redondances

En théorie, les redondances sont à proscrire pour éviter les incohérences. Mais un chaînage dans l'hypergraphe peut faire apparaître des cycles. Faut-il les "casser" en supprimant des liens ? Non bien sûr, on conservera toujours les liens qui sont soit des contraintes à vérifier impérativement, soit des informations indépendantes de l'échelle voire de la géométrie.

Par exemple, le lien "une route relie des villes" pourrait être supprimé lorsque l'on fait apparaître les classes géométriques car les surfaces qui représentent des "villes" sont bordées par des arcs reliés à d'autres arcs par des sommets, certains de ces arcs représentant des "tronçons de routes" composant les "routes". Cependant, la suppression de ce lien aurait deux inconvénients majeurs : la relation entre villes et routes serait difficile à exploiter et il serait nécessaire de faire apparaître les classes géométriques sur le modèle !

4) Une stratégie pour bien modéliser

Un modèle compliqué ne peut pas être facilement exploité, c'est-à-dire lu et encore moins mis en oeuvre dans un SIG. De plus, compliqué ne signifie pas nécessairement exhaustif !

4.1) Faire simple au début

La première recommandation est donc de faire au plus simple dans un premier temps. Ne pas commencer par dessiner des hyperclasses mais des classes avec éventuellement un attribut "type" d'objets qui pourra par la suite servir à décomposer la classe en une hyperclasse. Ne pas commencer par des attributs composés mais penser que chaque attribut pourra se décomposer.

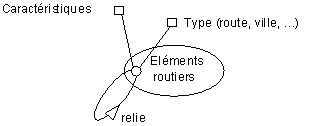
Ce modèle est un caricature mais constitue un bon début !

4.2) Identifier les réseaux géographiques

Les données géographiques sont souvent structurées en réseaux : le réseau routier, le réseau ferré, les réseaux de transport d'énergie (gaz, électricité, ...), les cours d'eau, ...

4.2.1) Identifier les nœuds de réseau

Il est souvent aisé de faire apparaître les éléments linéaires sous forme de classes reliées à des classes de nœuds de réseau. Ces nœuds correspondent à des connexions (voire à des intersections). Si on choisit de faire des thèmes, les nœuds peuvent s'appeler connexions, carrefours, franchissements (ponts,...), etc... Il est cependant plus facile de conserver la classe de nœuds et de la relier à des classes d'objets qui seront "localisés" par ces nœuds.

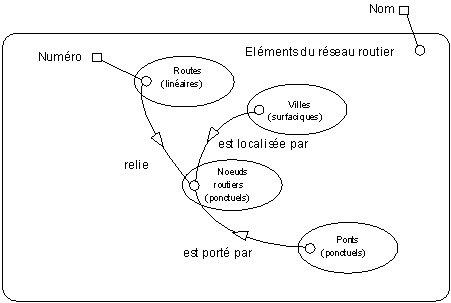
Par la suite, en fonction du MCD du SIG, on pourra soit considérer les objets portés par les nœuds comme des objets complexes, soit considérer qu'ils constituent une classe de nœuds particulière. On se souviendra que l'appellation "nœuds" ne signifie pas nécessairement "représenté par des sommets" : une ville est un nœud de connexion et pourtant elle sera représentée par une surface à une certaine échelle.

4.2.2) Identifier les tronçons

A l'instar de la notion de nœuds, la notion de tronçons est souvent d'un grand secours. Une route relie des villes mais croise d'autres routes. De plus, son nombre de voies n'est pas constant entre deux carrefours. Il est donc intéressant de considérer qu'entre deux nœuds, on a un tronçon (quitte à redéfinir les nœuds).

Remarque, si on considère que les nœuds et les tronçons n'ont pas de "nom", on peut les sortir de l'hyperclasse ...

4.2.3) Le problème de l'orientation d'un réseau et les attributs de lien

De nombreux réseaux possèdent un sens de parcours intrinsèque, par exemple : le sens d'écoulement de l'eau, le sens de circulation des automobiles. Pour faire apparaître sur le modèle cette notion (non visuelle !), on peut décider d'orienter les tronçons (linéaires) par rapport à la géométrie des arcs qui les représentent. On utilisera pour ce faire, la notion "d'attribut de lien".
 

L'attribut "sens" porté par le lien de représentation des "tronçons de routes" par les arcs indiquera pour chaque tronçon si l'arc peut être parcouru dans les deux sens ou dans un seul (en suivant l'ordre de la liste de coordonnées ou en la lisant à l'envers).     Un arc est toujours orienté car ses coordonnées constitue une liste ordonnée.

Attention, cette solution implique de préciser que les tronçons ne sont plus des tronçons de chaussées mais correspondent à un ensemble de voies de circulation dans un même sens et pour une même route.

Voici un exemple de route dont le nombre de voies de circulation varie :

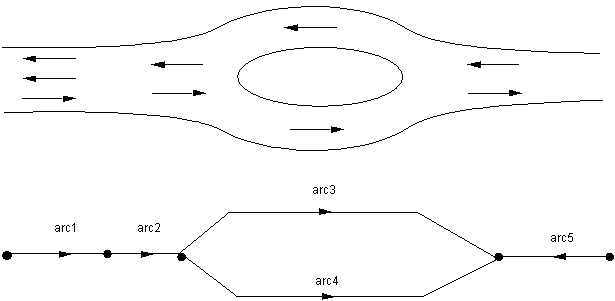
La route va pouvoir être représentée par 5 arcs grâce à 2 tronçons (à 1 et 2 voies) :
 

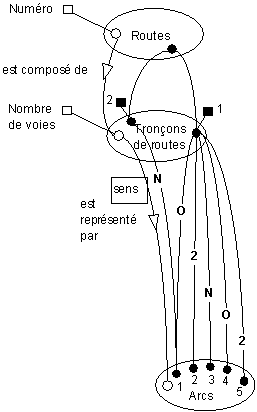On précisera dans le glossaire que l'attribut "sens" peut prendre les valeurs suivantes : - O : dans le sens de l'arc ; - N : dans le sens inverse de l'arc ; - 2 : dans les 2 sens.